AVENTURAS MATEMÁTICAS: mayo 2020

lunes, 25 de mayo de 2020

TEOREMA DE PITAGORAS Y EL TRIANGULO RECTÁNGULO

Antes de comenzar a hablar del Teorema de Pitágoras es interesante preguntarse ¿Quién es Pitágoras?

Pitágoras de Samos fue un filósofo y matemático griego nacido en el año 569 a.C. considerado el primer matemático puro de la historia. Contribuyo bastante en el avance de la matemática helénica, la geometría y aritmética.

Este filoso y matemático griego fue el creador del tan famoso Teorema de Pitágoras, que define que en todo triangulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir 90°.

QUE ES EL TEOREMA DE PITAGORAS ?

El Teorema de Pitágoras es un teorema que nos permite relacionar los tres lados de un triángulo rectángulo, por lo que es de enorme utilidad cuando conocemos dos de ellos y queremos saber el valor del tercero.

El descubrimiento del teorema de Pitágoras abrió un nuevo mundo en las matemáticas conocidas hasta ese tiempo y hasta el día de hoy nos sigue sorprendiendo y sirviendo de base para nuevas teorías que ayudan a que la humanidad se desarrolle cada vez más en un campo tan importante como es el de las matemáticas

*Triangulo Rectángulo

Cuando un triángulo dispone de un ángulo recto (que mide noventa grados), se lo clasifica como un triángulo rectángulo. Los otros dos ángulos del triángulo rectángulo siempre son agudos (miden menos de noventa grados).
El ángulo recto en el triángulo rectángulo está formado por los dos lados de menor longitud, conocidos como catetos, mientras que el tercer lado (el de mayor extensión) recibe el nombre de hipotenusa

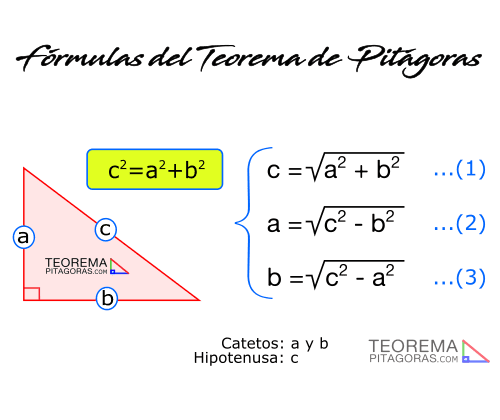
El teorema de Pítágoras relaciona los tres lados de un triángulo rectángulo (Catetos e Hipotenusa) mediante la siguiente fórmula:

c²= a²+ b²

Donde:

«c»: es la hipotenusa.
«a» y «b»: son los catetos.

De esta fórmula del teorema de Pitágoras podemos deducir las fórmulas para calcular el cateto y la hipotenusa directamente. Esto es una operación algebraica donde se despejan: «a», «b» y «c» y se obtiene las siguientes fórmulas:

El cuadrado de uno de los catetos es igual a la raíz cuadrada de la resta de la hipotenusa al cuadrado menos el otro cateto al cuadrado.

EJEMPLO:

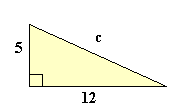
c²=a² + b²

c²=5² + 12²

c²=25 + 144

c² = 169

c = √169

c = 13

sábado, 9 de mayo de 2020

MEDIDAS DE ÁNGULOS

Los grados Sexagesimales

Grado sexagesimal - Wikipedia, la enciclopedia libre

El grado sexagesimal se define como una de las 360 partes iguales en las que se divide una circunferencia.

Cada grado sexagesimal se divide en 60 minutos, y cada minuto se divide en 60 segundos. Los grados, minutos y segundos se representan como:

$a^{\circ} \hspace{0.1cm} b^{'} \hspace{0.1cm} c^{''}$

Ejemplo :

$45^{\circ} \hspace{0.1cm} 5^{'} \hspace{0.1cm} 50^{''}$

Se lee 45 grados, 5 minutos, 50 segundos.

El Radián

▷ Cómo de hacer para pasar de grados a radianes

"Un radián es el ángulo central de una circunferencia que abarca un arco de igual longitud que el radio de la misma".

Al igual que podemos medir longitudes con metros o masas con gramos también podemos medir ángulos con radianes, expresándolo en ese caso con rad o sin nada.

El grado sexagesimal (o simplemente grado). La equivalencia entre estas dos medidas es la siguiente: $180^\circ=\pi \, rad$